AERODINÁMICA 2: EN BUSCA DE LA EFICIENCIA

Bienvenidos a la segunda entrega de mi serial sobre aerodinámica.  En el artículo anterior desgrané algunos de los conceptos que servirán de base para comprender mejor los efectos que el aire produce en su  tránsito a lo largo de un F1. Vimos qué es la aerodinámica, la definición de fluido y los diferentes factores que generan resistencia. Hoy quiero dar un paso más en este aspecto y centraré mis esfuerzos en describir uno de los factores más buscados y deseados en la competición: la eficiencia aerodinámica.

Como resumen de todo lo analizado en el artículo anterior decir que la resistencia aerodinámica está formada por dos componentes principales: la forma del cuerpo y la viscosidad del aire. Una predominará sobre la otra dependiendo del régimen de trabajo que tenga el objeto. Dependiendo de la forma que tenga el objeto y la velocidad del aire que pase junto a él, una predominará sobre la otra. Cuando la velocidad es baja produce más efectos de la viscosidad y a medida que se va incrementa la velocidad comienza a tener preponderancia la forma del cuerpo.
Todos sabemos los F1 actuales no son vehículos que podamos considerar lentos, por mucho que un suministrador de motores japonés se empeñe en que pensemos lo contrario, de ahí que se "desprecie" en parte el efecto que la viscosidad produce en el global de la resistencia y los ingenieros centren sus esfuerzos en pulir las formas para mejorar la eficiencia. No es para menos. Reducir la resistencia implica que el motor tenga que gastar menos potencia para conseguir ganar velocidad, afectando directamente al consumo. 
Uno de los puntos fuertes del equipo Mercedes es su eficiencia. Han sido capaces de encontrar un equilibrio perfecto entre generación de carga y reducción del drag empleando a su vez el propulsor más potente de la categoría. Esto les permite salir a pista con una cantidad inferior de combustible que la competencia, o en caso de llevar el mismo poder exprimir durante más tiempo el motor con la mejora en tiempo que ello supone.
Como vemos "pulir" el diseño aerodinámico tiene un valor vital en muchos sentidos. El primer mandamiento de un aerodinamista es encontrar la eficiencia y en la búsqueda de esa Quimera se emplean muchos recursos y horas de trabajo, pero realmente sabemos qué es la eficiencia aerodinámica.

Eficiencia aerodinámica.

Se denomina eficiencia aerodinámica a la relación entre el coeficiente de sustentación (CZ) y el coeficiente de resistencia aerodinámica (CX). ¡Ya empezamos con las palabritas raras! Estará pensando un buen amigo mío pero no asustaros que es más fácil de lo que parece. Vamos a verlos uno a uno.

Coeficiente de sustentación.

Para tener todos los conceptos bien claros decir que la sustentación es la fuerza perpendicular al avance generada sobre un cuerpo cuando se desplaza a través de un fluido. La forma más conocida es la producida por el ala de un avión o la de un ave.

Para saber si la superficie y el perfil de un ala genera mayor o menor  sustentación tendríamos que poder medirlo pero hay un pequeño problema, no hay forma de hacerlo directamente. La sustentación es una magnitud adimensional, es decir no tiene una dimensión física que podamos medir. ¿Qué quiere decir esto? Con un ejemplo lo entenderéis mejor.


Imaginaros que os pido que midáis un objeto; la puerta de vuestro dormitorio. Si queréis  obtener su altura utilizaréis un metro, para el peso una báscula, para saber su superficie solamente tendremos que medir alto y ancho  y aplicar una simple operación matemática. Como objeto que es, solamente tendremos que emplear los instrumentos de medición adecuados, realizar las medidas y obtendremos unos valores a los que asociaremos la unidad dimensional que le corresponda (centímetro, gramo, Km/h, atm, etc.).
En ciencias, una magnitud adimensional  es una cantidad, un número puro que no lleva asociada ninguna dimensión física pero nos sirve de ayuda a hora de describir una característica física. El coeficiente de  sustentación (CZ) es un claro ejemplo. En el caso que nos ocupa no existe ningún instrumento que pueda medir directamente su valor pero si podemos valorarlo numéricamente gracias a la medición de otras propiedades físicas que intervienen en la ecuación (presión, densidad, ángulo de ataque, superficie del ala, velocidad del fluido, etc.). El valor obtenido nos servirá para determinar la efectividad que tiene  la forma de un cuerpo para producir sustentación. Este valor es fundamental ya que se usa para facilitar los cálculos y el diseño de la pieza. 
Cuánto más alto sea el valor de CZ mayor sustentación producirá y viceversa, llegando incluso a alcanzar valores negativos. ¿Esto es un problema? Depende de lo que se esté diseñando. Si fuera pasajero de un avión y estuviera volando rezaría para que los valores fueran positivos, eso me indicaría que las fuerzas que actúan sobre el ala la empujarían verticalmente hacia arriba y podría volar con seguridad pero si fuera piloto de un F1 querría que los valores fueran los más negativos posibles. Cuando el valor es negativo las fuerzas que actúan impiden la sustentación. En este caso dichas fuerzas empujan hacia abajo produciendo uno de los efectos más deseados en la competición del motor, la carga aerodinámica (downforce).  

El coeficiente de resistencia aerodinámica (CX)

Es uno de los coeficiente más importante a la hora de diseñar cualquier componente de ingeniería que reciba los efectos de algún fluido en su estructura. Aquí no estoy hablando solo de competición. La construcción de un edificio o de un puente llevan asociado un estudio detallado que analice la resistencia que presenta las superficies que lo forman frente al aire para saber si se tendrán o no que reforzar sus estructuras en caso de tormentas, huracanes, etc.
El coeficiente de resistencia aerodinámica también es un número adimensional que viene determinado casi totalmente por la forma del objeto y sirve para cuantificar el arrastre o resistencia que presenta un objeto cuando está dentro de un fluido. Su valor depende de la resistencia de forma y  la fricción. 
Este coeficiente  siempre está asociado con una superficie particular. Un valor  bajo indica que el objeto tendrá menos resistencia que otro que lo tenga alto. En el siguiente esquema vemos  varios ejemplos. Un dato a tener en cuenta es que todas las figuras tienen la misma superficie frontal.

Si nos detenemos a analizar el esquema veremos varias combinaciones que  llaman mucho la atención. Resulta curioso ver como una semiesfera (objeto 2) es más eficiente aerodinámicamente hablando que la esfera (objeto 1). También llama la atención comprobar como el valor  Cx producido por un cilindro largo (objeto 6)  es mucho menor que si el cilindro es corto (objeto 7) a pesar de tener los dos la misma superficie que impacta contra el flujo. ¿A qué es debido esto? Se debe principalmente a la resistencia que producen las turbulencias situadas en la parte trasera del objeto, la famosa succión de cola que vimos en el artículo anterior. ¿Os acordáis? Sí, aquel  apartado que hablaba de la resistencia por presión. Pues nada, los que no se acuerden ya va siendo hora de que le deis un repaso. Seguimos.

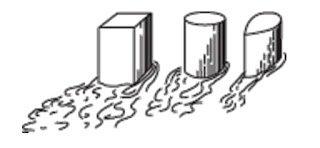
La forma que tiene un objeto definirá la trayectoria que tendrá que seguir el aire para poder rodearlo. Dependiendo de la velocidad y la ordenación con que lo haga, el aire saldrá del objeto de una manera ordenada o no dependiendo de sus diferentes trayectorias. Un ejemplo para verlo y para ello os enseñaré este dibujo.

En él se puede apreciar como tres objetos que tienen superficies frontales iguales van dejando tras de si una estela turbulenta diferente  cada uno. Cuanto mayor sea la estela, mayor resistencia  por presión producirá y por tanto el valor de Cx crecerá. De manera similar ocurriría con los cilindros. La figura alargada del cilindro con mayor longitud permite al aire sortear el objeto de forma más ordenada que en el caso del corto de ahí que su capa límite se desprenda más atrás originando un valor Cx bajo.
Sería conveniente recordar que en artículo anterior decía que lo más importante en el  diseño de un coche no era la parte delantera sino la  trasera, al contrario de lo que se podría esperar ya que su forma definía la capacidad que tenía el vehiculo de rellenar con aire  el vacío que dejaba tras de si al desprenderse la capa límite (concepto que veremos de manera extensa en la próxima entrega).
Si analizamos las formas geométricas que menor resistencia producen destacan sobre el resto dos figuras. Por un lado tenemos la geometría en forma de media lágrima  (Cx=0.09)  y la estrella de la lista, la forma de lágrima completa (Cx=0.04).
Resulta curioso ver como el sentido común va en contra de la realidad.  Para muchos, la mejor manera de disminuir la resistencia que ofrece el aire sería colocar el borde fino enfrentando a la corriente y el borde redondeado atrás, ya que de esa manera el cuerpo "corta" mejor el aire que se opone a su paso. El Ferrari  312 del año 1976 es un claro ejemplo de lo que estoy diciendo. Está forma se impuso en los años setenta en la F1 debido principalmente a mejorar el agarre gracias al efecto suelo pero la realidad es bien distinta.

Si se coloca el borde afilado hacia adelante, las partículas de aire van sufriendo un aumento paulatino de la presión hasta que el flujo se desprende formando torbellinos muy potentes. En aquellos años los estudios en aerodinámicas aún no estaban tan avanzados y de ahí que los diseñadores de la época dieran por válidos conceptos que hoy en día sabemos que no lo son.

Colocar el borde redondeado en la parte delantera crea una zona de bajas presiones que "atrapa" el aire y lo pega a la superficie (efecto coanda) haciendo que fluya casi sin dificultad corriente abajo hasta que en un determinado punto comienza a desprenderse, en concreto un poco antes del borde de la cola reduciendo así al mínimo la creación de torbellinos, como puede apreciarse en el gráfico.

Como sabemos la naturaleza es sabia y en ella podremos encontrar infinidad de ejemplos de animales y plantas que emplean esta geometría para reducir la resistencia. Si observamos a los peces comprobaremos que tienen  formas muy similares a estas. Después de millones de años de evolución se consiguió la forma ideal y nosotros solo teníamos que copiarla.
A simple vista podríamos pensar que no hay demasiadas similitudes entre una lágrima y un F1 salvo los ya conocidos, las alas que forman los alerones  pero no es así, si miramos detenidamente podremos encontrar más similitudes de las esperadas.
Si observamos un monoplaza lateralmente lo primero que nos llama la atención es que la geometría que forman los pontones que contienen los radiadores, la parte trasera de la carrocería y el suelo. ¡Qué curioso, parece mucho a una media lágrima! Sí, lo es, sobre todo en la zona más interna de la carrocería como vemos en la imagen del F14T que os muestro a continuación. La parte exterior de los pontones también tiene rasgos similares; forma redondeada, más ancho en el inicio que va disminuyendo de tamaño a medida que se acerca a la zaga del coche.

Si analizamos cómo ha cambiado esta zona a lo largo de los años veremos con claridad la evolución del diseño. En 1993 el Ferrari F93A mostraba una carrocería totalmente recta sobre los pontones, muy similar a la empleada por el Toyota TF103 en 2003. A partir de ahí se empezó a trabajar de manera intensa en la reducción de cualquier elemento que añadiera resistencia al monoplaza y para ello tuvieron que aerodinamizara todo el coche. Esa es las líneas a seguir desde entonces.
Si miramos los coches desde arriba la cosa cambia. Hay que remontarse al año 1985 para ver los primeros modelos que empezaban a utilizar la geometría en forma de lágrima en su carrocería. En 1981, el Ferrari 126C que pilotara Gilles Villeneuve tenía una planta totalmente rectangular que aumentaba al máximo la superficie del coche para potenciar el efecto suelo. Se tuvo que esperar hasta 1985 para empezar a ver los primeros diseños de monoplazas con la zaga ligeramente despejada. El Ferrari F93A, un coche que se "arrastró" por la pista allá por el año 1993 mostraba ya signos claros de la estilización en forma de lágrima pero muy lejos de los estándares actuales. Solo hace falta ver la figura estilizada del F150 para darse cuenta de lo que estoy diciendo.

Queda claro que  la geometría en forma de lágrima es el mejor aliado para los diseñadores que buscan la ansiada eficiencia.

¿Por qué es tan importante la eficiencia aerodinámica?

Bien. Ahora que ya conocemos los conceptos voy a entrar en la parte más importante del artículo. Como dije antes, la  eficiencia aerodinámica a la relación entre el coeficiente de sustentación (Cz) y el coeficiente de resistencia aerodinámica (Cx). Para obtenerlo sólo tenemos que dividir el valor del primero por el segundo y listo. El diseño ideal de un Fórmula 1 eficiente sería montar una serie de elementos aerodinámicos que creara valores Cz negativos muy altos unido a valores Cx cercanos a cero, pero eso no es posible en la realidad. Incrementar la sustentación produce un aumento en el arrastre.

La resistencia que se produce sobre cualquier objeto no es una constante. Este es un dato a tener muy en cuenta a la hora de comprender por qué es tan importante pulir un diseño que permita a los equipos obtener monoplazas con  elevada eficiencia aerodinámica (poca resistencia y mucha carga). Hasta ahora habíamos visto como la resistencia dependía de la forma del objeto, su posición, de la densidad del fluido y pero nos falta el factor más importante de esta ecuación: la velocidad. 
Para los que odian la física y las matemáticas este esquema que os muestro a continuación le parecerá chino pero es importante para comprender los efectos que la velocidad produce. Como siempre luego usaré un ejemplo para intentar aclarar los conceptos.

Esta ecuación quiere decir, traducido a un idioma más comprensible que la resistencia aerodinámica es  proporcional al cuadrado de la velocidad relativa entre el objeto y el fluido. En condiciones normales la densidad de aire no va a variar. Tanto la superficie que presenta el frontal de vehículo como su coeficiente aerodinámico no variarán tampoco salvo en los momentos en que el piloto activa el DRS pero descartaremos esta posibilidad para facilitar la taréa. Por tanto  a la hora de hacer los cálculos lo único que sí puede hacer variar la resistencia es modificar  la velocidad, y doy fe que produce efectos muy importantes. Vamos a verlo.

Imaginaros que circulamos en un Audi A3 del año 2006 (Cx=0.32) a una velocidad sostenida de 50 km/h en un tramo horizontal y sin viento. Al moverse, la carrocería tiene que desplazar una cantidad de aire determinada y necesita para hacerlo 1.2  CV (caballos de potencia). Vemos que hay otro vehículo delante y nuestro espíritu competitivo nos insta a querer adelantarlo. Pisamos el acelerador y alcanzamos los 100 km/h. Algunos pensarán; si  doblamos la velocidad la resistencia también se multiplica por 2 pero no, no es así, realmente lo hacemos por 4. Es cierto que sobre el frontal del coche golpea el  doble de aire que a 50 km/h pero también es cierto que lo hace con el doble de fuerza de ahí que el coche necesite multiplicar  considerablemente la potencia para poder circular a esa velocidad, en concreto x8. En estas condiciones necesitamos unos 9.6 CV para circular a 100 km/h.
En un ataque de locura cogemos con firmaza el volante  y ponemos nuestro coche a 200 km/h. La cosa se dispara. Serían necesarios 77 CV para mantenernos y a  300 km/h ni os cuento, la friolera de 259 CV. Los datos de la potencia surgen fácilmente de aplicar su ecuación física (Potencia = Fuerza (en este caso los valores de la resistencia) x Velocidad) por si alguien se anima a volver a calcularlo como yo.

Como vemos, la resistencia aerodinámica se incrementa mucho más deprisa que la velocidad y eso repercute en las necesidades de potencia y sobre todo en el combustible. A menor potencia consumida, menor gasto de combustible. Sólo un dato, pasar de 110 a 120 km/h incrementa el consumo de un coche de calle una media de 15 %. Este factor es de vital importancia, sobre todo cuando compites en un certamen donde los niveles carga de carburante está limitados por normativa (100 Kg. por carrera). Un coche poco eficiente tendrá que estar ahorrando gasolina durante mucho más tiempo que otro que si lo es. Antes de entrar en escena la limitación también generaban problemas el exceso de consumo. Los monoplazas que más consumían tenían que saltar a pista con sobrepeso, lastrando los tiempos por vueltas sobre todo en la primera fase de la carrera. Veis la importancia de este asunto.

Extrapolando  estos datos a un F1 voy a intentar demostrar por qué hay coches con unidades de potencia de Mercedes que no son capaces de ahorrar tanto combustible y menos conseguir las prestaciones en pista que dan las flechas plateadas. Voy a dar por hecho que a estas alturas de la película, quién más, quién menos ya ha podido obtener todo o casi todo el rendimiento que da la Unidad de Potencia alemana para descartar que las carencias se deban a este factor. El año pasado había dudas de si los equipos clientes podían exprimir al 100 % la energía creada por el propulsor pero pasados más de un año de experiencia yo creo que todos lo habrán conseguido. Entonces ¿Por qué tanta diferencia? La clave puede estar en un factor: en el coeficiente de resistencia (Cx). Vamos al lío.
Los valores Cx de un F1 varían dependiendo de las necesidades de carga que necesite el coche  pero más o menos rondan entre el 0.7 para Monza y el 1.1 en Mónaco.  Estos valores son aproximados y dependen tanto de la configuración específica de cada equipo y como de lo acertado que sea el diseño pero cualquier mínima variación produce efectos destacados.
Para que veáis con claridad cómo afectan estas variaciones en el rendimiento os he preparado esta tabla. En ella aparecen los resultados obtenidos en el ejemplo anterior y he añadido dos ligeras modificaciones tanto para baja  como  para alta carga. Los resultados hablan por si solos.

Una variación muy pequeña, en torno a las dos centésimas en una pista de baja carga como puede ser Monza  equivale a necesitar 25 CV de potencia menos que tus rivales en las rectas para alcanzar los 300 Km/h. Si el circuito es de alta carga, una variación "grande" dispara las diferencias entre los equipos. Podéis comprobar que con sólo  una  décima, los valores de potencia necesarias a máxima velocidad difieren en casi 80 CV. Es difícil ver variaciones entre los equipos superiores a esa décima pero se pueden dar.
Hasta ahora todas las necesidades de potencias analizadas se deben a la acción del aire y la resistencia que genera pero no son las únicas. Existen otros elementos que también producen arrastre y que aumentan el consumo de potencia  como puede ser el contacto de las ruedas con el suelo (arrastre mecánico), el rozamiento de los elementos mecánicos, etc.
Si extrapolamos estos datos es fácil deducir el porqué del dominio del equipo Mercedes. Sí, es verdad que disponen de la mejor unidad de potencia de la categoría, que exprime mejor que nadie toda la capacidad de recuperación de energía del MGU-H pero no sólo de motor vive la F1. Obtener habitualmente  diferencias superiores al segundo por vuelta con respecto a equipos que llevan el mismo corazón en su interior conducen obligatoriamente a pensar que la eficiencia aerodinámica de las flechas de plata es  mejor que la de sus rivales.
Bueno amig@s, hasta aquí lo que se daba. En la próxima entrega analizaré dos de los elementos más importantes en la aerodinámica de un F1: el concepto  de capa límite y el efecto Coanda pero antes os quiero mostrar algunos ejemplos de diseños extremos que intentaron encontrar la tan deseada eficiencia. Espero que os resulte interesante, pero eso será otra historia.